Принцип работы ускорителей.
Прямых опытов, подтверждающих именно рост энергии до миллионов и миллиардов электронвольт, никто не проводил. До сих пор энергию ускоренных частиц определяют как:
а) суммарное число раз пролёта частицей заданной разности потенциалов;
Этот способ является основным при работе ускорителей. Он основан на ошибочном представлении, что заряд ускоряемой частицы не меняется от скорости, что произведение тока на напряжение, а это и есть энергия, от скорости не меняется.
Электрическое поле для заряда является не чем иным, как ветром для парусника. Парусник не может двигаться быстрее ветра. Электрическое поле имеет конечную скорость распространения – это скорость света. Поэтому, при приближении скорости частицы к скорости света, она, вообще, перестаёт ускоряться, независимо ни от массы, ни от величины заряда. Аналогично и магнитное поле перестаёт поворачивать частицу.
Следовательно, этот способ подсчёта энергии ускоряемых частиц является порочным с точки зрения обычной физической логики.
б) длиной пробега частицей в пузырьковой камере в сочетании с магнитным полем, воздействующим на частицу, если она имеет заряд;
Этот способ появился раньше изобретения ускорителей, для исследования космических лучей и радиоактивных элементов. Поэтому, когда появились ускорители, появилась возможность получать частицы с такой же длиной пробега и идентифицировать их энергию, вышеназванным способом.
в) толщиной поглощающего материала;
Этот способ также связан с работой ускорителей, когда появилась возможность получать частицы с разной энергией и исследовать их проникающую способность. Эти энергии опять же считаются как произведение заряда на общую разность потенциалов, т.е. тем же порочным способом.
Все оказались под действием гипноза
«великого творения А.Эйнштейна», беспрекословно уверовав в его правильности.
Измерение радиуса отклонения быстрых электронов в магнитном поле вроде бы
«подтвердили» вывод Эйнштейна о зависимости массы от скорости. На этом по сути всё и закончилось. Единственная попытка прояснить ситуацию в
этом направлении закончилась опять же ошибочным выводом. Эту попытку сделал
Бертози, который исследовал зависимость скорости электронов от их
кинетической энергии и наличие верхней границы для этой скорости. Описание
этого опыта привожу из книги У.И.Франкфурта «Специальная и общая теория
относительности»: «Пучёк электронов из генератора Ван де-Граафа направлялся в
линейный ускоритель (Массачусетского технологического института); выходящие
электроны обладали кинетической энергией в интервале 0,5 – 15 Мэв. Поскольку проверялось одно из основных соотношений релятивизма, все
величины определялись по возможности прямыми методами. Скорость определялась
непосредственно по времени прохождения электроном заданного расстояния, а кинетическая
энергия – калориметрическим путём, по нагреванию алюминиевого диска, в котором
тормозились электроны. Строились кривые зависимости (v/c)2 от
Ek/m0c2 (Ek – кинетическая
энергия, m0 – собственная масса
электрона).
Классическая механика даёт : (v/c)2
= 2Ek/m0c2, т.е. линейную зависимость, а релятивистская: (v/c)2
= 1 – 1/(Ek/m0c2 + 1)2.
Экспериментальные данные хорошо
накладывались на релятивистскую кривую, и хотя точность эксперимента не очень
велика (10%), он однозначно определяет существование верхнего предела для
скорости электронов.» У.И.Франкфурт
упростил задачу опыта. Основной задачей опыта и для этой цели был применён калориметрический метод измерения кинетической энергии
являлось доказательство независимости
силы электрического поля от скорости электронов, т.е. формулы Ek= eU.
Рассмотрим механизм ускорения электрона в циклотроне. Линейный ускоритель в этом плане принципиально мало чем отличается от циклотрона, поскольку его длина разделена на множество ускоряющих промежутков, что равнозначно заменяется количеством оборотов в циклотроне. Выше я уже говорил, что теория Эйнштейна хотя и утверждает конечность скорости и света и электрического поля, в динамике она этот фактор не учитывает. До сих пор бытует мнение, что заряд, пройдя определённую разность потенциалов, приобретает энергию, равную произведению заряда е на напряжение U. Вся электротехника зиждется на этой формуле и даёт прекрасные результаты. Но, эта формула верна не во всех случаях жизни, а лишь при малых скоростях электронов. В ускорителях частицы разгоняются до скоростей, близких к скорости света и там действуют уже другие законы. Во-первых, на заряд действует электрическое поле не со скоростью с, а со скоростью c – v. Поэтому, ускорение, приобретаемое электроном при той же разности потенциалов, уменьшается в соответствии с коэффициентом (c – v)/c или
(1 – v/c). Во-вторых, сюда добавляется ещё уменьшение
скорости взаимодействия самого заряда с электрическим полем в соответствии с
коэффициентом 
. Этот коэффициент действует и в магнитном
поле, удерживающем заряд на орбите. И общий коэффициент к ускорению
становится (1-v/c) . Это не Эйнштейновский коэффициент (1-v2/c2) , не отражающий никакой физической сути.
Теперь
рассмотрим работу циклотрона, основываясь на ясном физическом принципе его
работы.
Итак, заряд электрона е = 4,803∙10-10ед.СГСЭ, 1электронвольт
= 1,602∙10-12эрг.
Возьмём ускоряющий зазор = 1см и
напряжение 1вольт. Деля энергию на расстояние найдём
действующую силу: 1,602∙10-12:1
= 1,602∙10-12дин. Разделив силу на массу
электрона, найдём ускорение: а
= 1,602 ∙ 10-12/ 9,1096 ∙ 10-28 = 0,176
∙ 1016 = 1,76∙1015см/сек2. Увеличим напряжение до
1000вольт, тогда а
= 1,76∙1018см/сек2.
Определим время пролёта электроном
1см и найдём полученную скорость:
S = at2/2; t2 = 2S/a; V1= at; t2= 2/1,76∙1018=
1,136∙10-18; t = 1,066∙10-9сек.
V1= 1,76∙1018×1,066∙10-9
= 1,876∙109см/сек.
Попав в ускоряющее поле, скорость
электрона выросла от 0 до 1,876∙109см/сек.
Сделав полуоборот, электрон опять
попадает в то же электрическое поле, но оно уже будет толкать его не со скоростью
с, а со скоростью с-v, т.е. сила, и, следовательно, ускорение уменьшатся в (c – v)/c раз. Найдём этот коэффициент: (3∙1010- 0,1876∙1010)/3∙1010
= 0,937. Найдём
новое ускорение: а2
= 1,76∙0,937∙1018= 1,65∙1018см/сек2.
Время t2
, будем искать из уравнения: at2/2 + v0 t -1 = 0, (v0 – скорость электрона после
предыдущего ускорения) подставляя сюда полученные значения a и v0. 1,65∙1018t2 + 2∙1,876∙109t – 2 = 0. Если у вас есть
Mathcad, то мы получим t2
= 4,45∙10-10сек. Определим прирост скорости за счёт ускорения а2:
V2 = a2t2 = 1,65∙1018∙4,45∙10-10
= 7,34∙108см/сек. После двух ускорений скорость электрона
выросла до V1+V2 = 1,876∙109
+ 0,734∙109 = 2,61∙109см/сек.
Вновь вычисляем коэффициент к ускорению: (3∙1010-0,26∙1010)/3∙1010=
0,91.
Вычислим ускорение: а3
= 1,76∙1018∙0,91 = 1,6∙1018см/сек2. Найдём t3.
1,6∙1018t2 +2×2,61∙109t – 2 = 0, t3 = 3,46∙10-10, V3= 5,54∙108см/сек.
V3общ
= V1+V2+V3= 3,164∙109см/сек.
Следует отметить, что полученные начальные
скорости совпадают со скоростями, полученными из другой формулы: V = (2Ek/mэ)0,5. Здесь Ек-
кинетическая энергия в электронвольтах, преобразованных в эрги, mэ – масса электрона. Эта формула из книги Дж.Б.Мэриона «Физика и физический мир». Она приближённая, для
малых скоростей. Для нашего случая:
Ек=
1000эв = 1,602×10-9эрг, mэ
= 9,1096×10-28г.
V1= 1,875×109см/сек.
V2= 2,65×109см/сек. V3= 3,248×109см/сек. Здесь я не учитывал коэффициента 
ввиду его малости,
но в дальнейшем он внесёт свою лепту в общий результат. Следовательно, при
малых скоростях кинетическая энергия равна энергии, приобретаемой электроном
в электрическом поле. Это совпадение подтверждает и правильность нашего метода
вычисления скорости. Но это совпадение наблюдается только на начальной стадии
разгона. В дальнейшем, по мере роста скорости частицы, эта формула начинает
увеличивать ошибку.
Mathcad позволяет автоматизировать процесс вычислений для любого
количества ускорений: привожу программу вычислений и некоторые сравнительные
результаты.
Кстати, по этой программе легко
перейти к вычислению скоростей по формуле А.Эйнштейна, заменив коэффициент
(1-v/c) на (1-v2/c2). Отличие
моего коэффициента от Эйнштейновского заключается
в том, что по его коэффициенту скорость растёт быстрее, чем по моему. Так
как v/c > v2/c2, если v/c < 1.
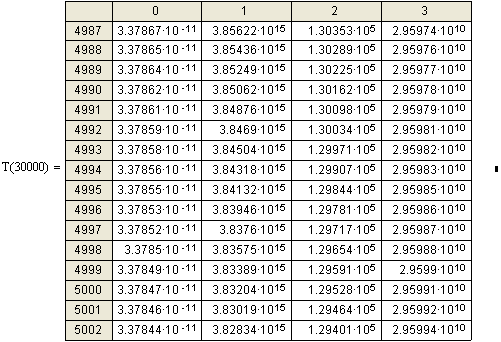
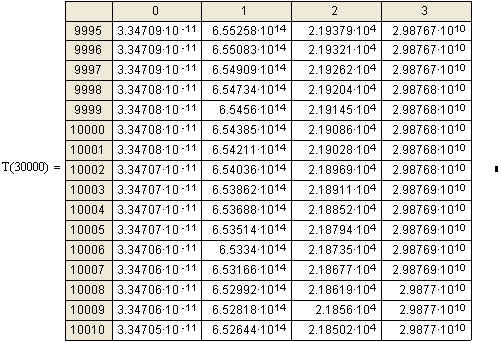
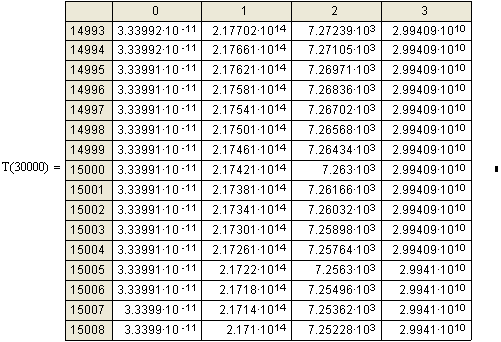
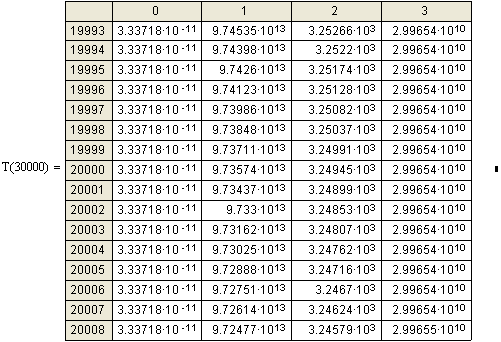
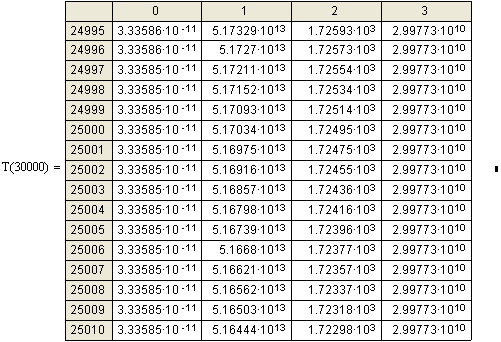
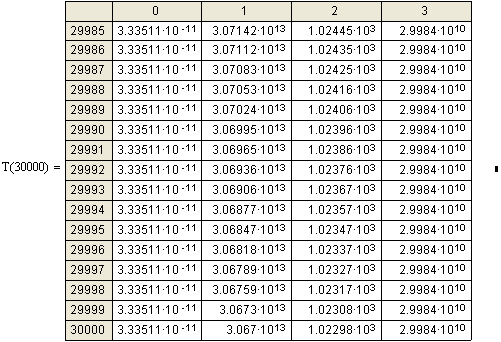
Если Бертози ускорял электроны
до 15 Мэв, то мой расчёт
простирается до 30 Мэв. Из
таблиц видно, что при приближении скорости электронов к скорости света, прирост
скорости с каждым новым ускорением становится всё меньше и меньше. Если вначале
разгона прирост скорости от 1000 эв V1 составлял: 7,341×108; 5,544×108; 4,6×108
см/сек, т.е. 7341; 5544;
4600 км/сек, то после 30000 ускорений этот прирост упал
до 10 м/сек.